I recently added a Tenma 72-14110 signal generator to my array of lab equipment. This handy waveform generator has quite a nice array of functions, such as the normal waveform generators, up to 5MHz, as well as arbitrary waveform generation, modulation, frequency counting, etc.
One function it has that I'd really like to use is the USB connection. But as usual the software that comes with it is nothing more than a crappy windows application that remote controls it and displays what's on the screen. So, time to do some hacking.
My requirements are simple: capture what's on the screen and output it as a PNG file. But with zero documentation that's going to be a fun job. So, now to crack out Wireshark. I'm running the bundled software in a Windows VM and using Linux on the host computer to capture the USB traffic. And straight away I can see a pretty simple pattern.
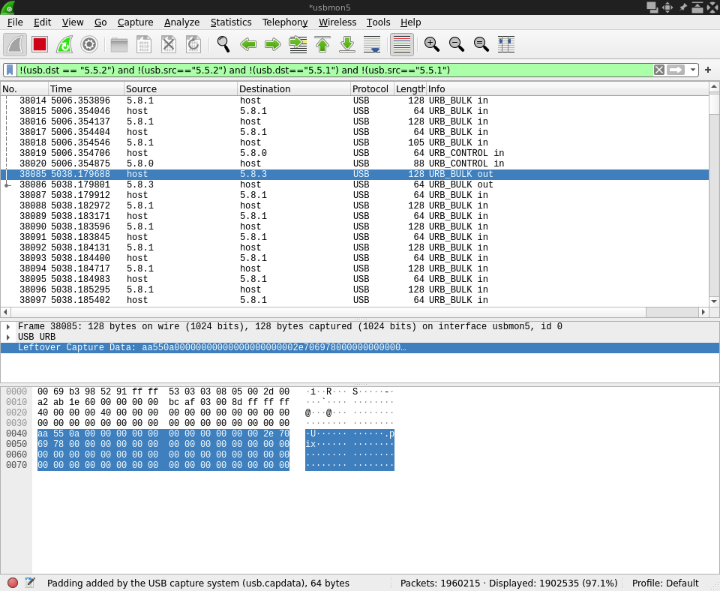
A request gets sent out by the computer, and a whole bunch of responses flood back in with the image data in it. That's pretty normal for this kind of device - my Tenma oscilloscope does something very similar, though the requests and responses are very different.
Now the real fun begins. Knocking up a small program in C using libusb is pretty simple and straight forward, so I did just and made it send the request to get a screenshot. And the data flooded in. Dumping that raw data to a disk file then let me examine it in more detail. And that's where the fun really starts.
How do you go about decoding some random image data where you have no clue what format it might be in? Well, that's when you need to look for clues and hints to point you in the right direction.
One major hint was that the amount of data that was spewed back changed depending on what was being shown on the screen. Not by a huge amount, but still it changed. If it were just raw data you'd expect it to always be the same size - that size dictated by the resolution of the display. But this changing size indicated that there must be some kind of encoding going on. Some form of compression. And my first guess, because it's by far the simplest compression method to implement, is RLE: Run-Length Encoding.
A second hint was handed me when I started examining the data itself with a hex dump (xxd). The first chunk of data never seemed to change:
00000000: efcd ab89 1000 0001 7f00 0000 0000 0000 ................
00000010: 0000 e003 007c e003 ff7f 9452 e07f 4a29 .....|.....R..J)
00000020: 630c 524a 5a6b ff7f 007c e07f ef41 f041 c.RJZk...|...A.A
00000030: ef3d 3632 3732 3636 343a 353a 0f42 c618 .=6272664:5:.B..
00000040: ce39 2925 ad35 8c31 6e25 563e 553e b02d .9)%.5.1n%V>U>.-
00000050: 3536 fd4a dc46 783a f431 f629 9419 b41d 56.J.Fx:.1.)....
00000060: b419 d525 1432 162e d521 b51d f529 1532 ...%.2...!...).2
00000070: b31d 931d ec10 0c11 6f21 4208 2104 8410 ........o!B.!...
00000080: b556 d65a 1042 7b6f 9c73 f75e 3146 734e .V.Z.B{o.s.^1FsN
00000090: 3967 a514 0821 6b2d e71c 8310 1f03 0000 9g...!k-........
000000a0: 0000 0000 0000 0000 0000 0000 0000 0000 ................
000000b0: 0000 0000 0000 0000 0000 0000 0000 0000 ................
000000c0: 0000 0000 0000 0000 0000 0000 0000 0000 ................
000000d0: 0000 0000 0000 0000 0000 0000 0000 0000 ................
000000e0: 0000 0000 0000 0000 0000 0000 0000 0000 ................
000000f0: 0000 0000 0000 0000 0000 0000 0000 0000 ................
00000100: ff97 c517 a980 ff97 c597 a980 ff97 c597 ................
00000110: a980 ff97 c597 8100 a735 8080 ff97 c597 .........5......
00000120: 8080 35a7 1736 00ff 97c5 9780 8035 a717 ..5..6.......5..
00000130: 3600 ff97 c597 8080 35a7 1736 00ff 97c5 6.......5..6....
Those first few bytes, if you twist them around as little-endian, spell out 0x89abcdef - that smacks of a "magic number" to me; something to identify this as the start of the image data. At first glance the rest just looks like garbage. But then it struck me: with all those zeros in there, if this was run-length encoded, that would be wasted space. So it must be something that's not part of the image data. But what could it be? My immediate thought was that it was a palette. The list of colours in an indexed image. After a bit of experimenting with different bit arrangements I found that yes, it is the palette. From 0x10 to 0xff are 120 colours as RGB555 format in little-endian 16-bit words. The big breakthrough came when I took a screenshot of the bundled software using Gimp and zoomed in and took some samples of the colours being displayed. I found that white was #f8f8f8, and after byte-swapping and splitting the components out and re-scaling, that is exactly what ff7f at 0x26-0x27 is.
A little bit of software fiddling later and I have all the colours decoded.
The real fun is really only just starting though. We've done all the easy bits: now to tackle the image data itself. And this was a doozey!
- Assumption: it's RLE encoded.
- Observation: the first three lines of the display are all the same
And in the data, from 0x100 onwards, we see some almost repeated patterns.
ff97 c517 a980 ff97 c597 a980 ff97 c597 a980 ff97 c597 8100 a735 8080 ff97 c597 8080 35a7 1736 00
Assuming that ff97c5 somehow marks the start of each line, since each line starts with the same colour, I think we have our first three repeated lines there. Now those three lines are made up of a very simple pattern: 396 pixels of greyish brown, and 84 of black, making 480 in total. Now, making another assumption that the RLE encoding in use can't handle more than 256 pixels in a row, we can guess that each of those three rows is made up of three RLE blocks: two brown and one black. Which, with 6 bytes to play with that splits them up nicely into three groups of two bytes.
Now the encoding scheme is going to need some way of identifying if any given byte is the start of an RLE run or just a simple pixel. Since we have less than 127 possible colours in our palette it's a safe enough bet that the highest bit in a byte is used for that purpose. Also since almost every one of those bytes in the snippet above have that bit set. Certainly the first of each pair has it set. The harder one to think about is the fifth line, which needs splitting up a little differently, like this:
ff97 c597 8080 35 a717 36 00
And if we examine the captured image we can see that there are indeed some individual pixels in that row which won't be RLE encoded. Another good pointer is that the 97, if you AND it with 0x7F to remove the highest bit, gives you 0x17, which if you look it up in the palette gives you the exact same colour as the button backgrounds. So we're really on to something there.
So we think we know how it works now - let's do a little bit of maths to see if our thinking is right.
Assumption: byte pairs - first is RLE (if high bit set), second is palette index. Assumption: High bits need masking out to get the actual data.
Taking the first line and masking out the high bit of each byte we get: 127 pixels of index 0x17, 69 pixels of index 0x17, 41 pixels of index 0x00. Adding up all the pixel counts gives us 237. Um. That's not right. That's less than half the number of pixels we'd expect. Another problem: if we only have 0-127 in our run length count there's no way we can do a whole line in just three blocks. Time for a re-think.
We're going to at least need to double the value. So we'll try that. 254 + 138 + 82 = 474. Still 2 short of the required 480 for this display. But we're so close.
Time for another assumtion: a run length of 0 or 1 is never going to happen. How about if we add 2 to each (i.e., 1 before doubling)? Well, that would bring us immediately to 480. Bingo. So we think we've cracked it. Let's try it out on one of the other lines:
ff97 c597 8100 a735 8080
For each pair take the first, mask off the highest bit, add one, and double. ff c5 81 a7 80 becomes 7f 45 01 27 00. Add one becomes 80 46 02 28 01 and double them makes them 100 8c 04 4e 02. Adding them gives us 0x1e0, which in decimal is that magical number 480.
We're on a roll here. Time to write a program to create an image and see what we get...

Oh dear. And we were going so well. We can begin to see the shape of the output, but it's really not right. Something must be up with our calculation. Let's take the next line and see what happens.
ff97 c597 8080 35 a717 36 00
This one's slightly trickier - we've got some individual pixels in the mix here. So let's do the same maths as we did above - mask, add one, double. In decimal that gives us: 256, 140, 2, 1, 80, 1, 1. Add them together: 481
Damn - one more than there should be. And yes, if we're always doubling and adding two, or adding one then doubling, we can never have an odd number in our run lengths. Which makes sense. So what's going on? How can we get an odd number? Hang on a minute. There's something odd about those numbers. All the others in the run lengths have had the upper bit set in both the run length count and the palette index. There's one here that doesn't: a717. Maybe that has something to do with it. Maybe if we take the run length, double it, then add either 1 or 2 depending on if that bit is clear or set, it may do something? Certainly on this row it would cause the total to go down by one, which is what we want. Time to try it out:
Result! It only took me a day!
So, to recap:
- Bytes 0x00 to 0x0f are unknown header information
- Bytes 0x10 to 0xFF are palette in 16-bit little-endian RGB555 format
- All subsequent bytes are image data, where you:
- Take each byte in turn.
- If the high bit is set,
- mask it out, then double the value
- Take the next byte. If the high bit is set, add 2 to the run length. If it's not set add 1.
- Draw the specified number of pixels in the colour of the (masked) second byte.
- If the high bit is not set just draw one pixel in the index colour of this byte.
And for reference here is my (rather bad) test program. I'm going to roll this into my tenma library now.
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <libusb.h>
#include <string.h>
#include <assert.h>
#include <gd.h>
const uint16_t vid = 0x5345;
const uint16_t pid = 0x1234;
#define BULK_EP_IN 0x81
#define BULK_EP_OUT 0x03
#define REQ_MODEL "\xaa\x55\x05\x00\x00\x00\x02\x09\x36\x00\x00\x00\x00\x00" \
"\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00" \
"\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00" \
"\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00" \
"\x00\x00\x00\x00\x00\x00\x00\x00"
#define REQ_TIMERLOCK "\xaa\x55\x01\x00\xff\x00\xff\xef\x36\x00\xff\x00\x00" \
"\x00\x74\x69\x6d\x65\x72\x20\x6c\x6f\x63\x6b\x00\x00" \
"\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00" \
"\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00" \
"\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00"
#define REQ_PIX "\xaa\x55\x0a\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00" \
"\x2e\x70\x69\x78\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00" \
"\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00" \
"\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00" \
"\x00\x00\x00\x00\x00\x00\x00\x00"
libusb_context *ctx;
libusb_device_handle *handle;
struct image {
uint32_t magic; // 89abcdef
uint16_t unknown[6];
uint16_t color[120];
uint8_t data[480 * 272]; // worst case scenario, no compression
} __attribute__((packed));
int x = 0;
int y = 0;
int colors[120];
void pushPixel(gdImagePtr img, int col) {
gdImageSetPixel(img, x, y, colors[col]);
x++;
if (x >= 480) {
x = 0;
y++;
}
}
int main() {
libusb_init(&ctx);
handle = libusb_open_device_with_vid_pid(ctx, vid, pid);
if (!handle) {
printf("Unable to open a device with VID 0x%04x and PID 0x%04x\n", vid, pid);
return -1;
}
if (libusb_detach_kernel_driver(handle, 0) != 0) {
printf("Unable to detach kernel driver\n");
libusb_attach_kernel_driver(handle, 0);
return -1;
}
if (libusb_claim_interface(handle, 0) != 0) {
printf("Unable to claim interface\n");
return -1;
}
int len;
if (libusb_bulk_transfer(handle, BULK_EP_OUT, REQ_PIX, 64, &len, 0) != 0) {
printf("Unable to send packet\n");
} else {
struct image incoming;
int err;
int i, j;
len = 64;
int tot = 0;
do {
if ((err = libusb_bulk_transfer(handle, BULK_EP_IN,
(uint8_t *)&incoming + tot, 64, &len, 10000)) == 0) {
tot += len;
}
} while (len == 64);
gdImagePtr img = gdImageCreateTrueColor(480, 272);
for (i = 0; i < 120; i++) {
colors[i] = gdImageColorAllocate(img,
(incoming.color[i] & 0x7c00) >> 7,
(incoming.color[i] & 0x3e0) >> 2,
(incoming.color[i] & 0x1f) << 3);
}
gdImageFilledRectangle(img, 0, 0, 480, 272, colors[0]);
tot -= 256;
i = 0;
while (i < tot) {
if ((incoming.data[i] & 0x80) == 0) {
pushPixel(img, incoming.data[i]);
i++;
} else {
uint16_t rle = incoming.data[i];
i++;
uint8_t col = incoming.data[i];
i++;
rle &= 0x7f;
rle <<= 1;
if (col & 0x80) {
rle += 2;
} else {
rle += 1;
}
col &= 0x7F;
for (j = 0; j < rle; j++) {
pushPixel(img, col);
}
}
}
FILE *file = fopen("tenma-dso.png", "w");
gdImagePng(img, file);
fclose(file);
gdImageDestroy(img);
}
if (libusb_release_interface(handle, 0) != 0) {
printf("Unable to release interface\n");
return -1;
}
if (libusb_attach_kernel_driver(handle, 0) != 0) {
printf("Unable to attach kernel driver\n");
return -1;
}
libusb_exit(ctx);
return 0;
}
And a little Makefile for it (assuming it's saved as dso.c):
CFLAGS=`pkg-config --cflags libusb-1.0 gdlib`
LDFLAGS=`pkg-config --libs libusb-1.0 gdlib`
dsg: dsg.o
cc -o dsg dsg.o ${CFLAGS} ${LDFLAGS}